|
Size: 605
Comment: converted to 1.6 markup
|
← Revision 5 as of 2012-05-14 11:04:18 ⇥
Size: 611
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| InformationTheory에서 각 심볼의 발생[Probability]로 유도되는 [Entropy] 함수. | InformationTheory에서 각 심볼의 발생[[Probability]]로 유도되는 [[Entropy]] 함수. |
| Line 3: | Line 3: |
| Zero-memory binary information source에서 S={0,1}로 주어질때 0과 1의 발생[Probability]를 p,q로 놓으면 p+q=1를 통해, p만의 함수를 유도할 수 있다. | Zero-memory binary information source에서 S={0,1}로 주어질때 0과 1의 발생[[Probability]]를 p,q로 놓으면 p+q=1를 통해, p만의 함수를 유도할 수 있다. |
InformationTheory에서 각 심볼의 발생Probability로 유도되는 Entropy 함수.
Zero-memory binary information source에서 S={0,1}로 주어질때 0과 1의 발생Probability를 p,q로 놓으면 p+q=1를 통해, p만의 함수를 유도할 수 있다.
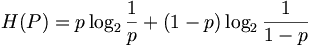
이를 그래프로 그려보면, /log(2))+((1-x)*log(1/(1-x))/log(2))
set ylab "H(x)"
set xlab "x"
set nokey
plot [0:1](x*log(1/x)/log(2))+((1-x)*log(1/(1-x))/log(2))](/wiki/EntropyFunction?action=AttachFile&do=get&target=e57c50efd0da62ae1db0714d83774e77529cfb3f_gnuplot.png)
즉, 확률p가 0혹은 1인경우 정보량은 0이며, 1/2인경우 최대값 1이된다.
 BioHackersNet
BioHackersNet