SimpleRegressionAnalysis

Simple RegressionAnalysis 단순회귀분석.

독립변수 하나와 종속변수 하나의 선형관계 분석. 회귀선이 직선이 되므로, straight-line regression이라고도 한다.

두 변수 x와 y간의 n개의 데이터(xi, yi), i=1,2,...,n 에 관한 직선회귀 모형은 다음처럼 표현된다.

$y_i = \beta_0 + \beta_1 x_i + \epsilon_i$

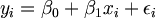
미지의 모수 beta_0, beta_1의 추정은 LeastSquaresMethod에 의해 구한다. 즉 오차 epsilon_i의 제곱의 합

$S = \sum_{i=i}^n {\epsilon_i}^2 = \sum_i(y_i-\beta_0 - \beta_1 x_i)^2$

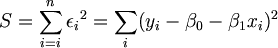
을 최소로 하는 beta_0, beta_1을 구하는 방법이다. 따라서 이 S를 beta_0와 beta_1에 대해 각각 편미분하여 다음결과를 얻는다.

$\frac{ \partial S }{ \partial \beta_0 } = -2 \sum_i(y_i - \beta_0 - \beta_1 x_i) \qquad \frac{ \partial S }{ \partial \beta_1 } = -2 \sum x_i(y_i - \beta_0 - \beta_1 x_i)$

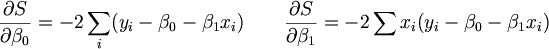
위의 편미분값을 0으로 만드는 beta_0와 beta_1의 추정값에 hat을 씌워 위 식을 정리하면

$n \hat{\beta_0} + \hat{\beta_1} \sum x_i = \sum y_i \qquad \hat{\beta_0} \sum x_i + \hat{\beta_1} \sum {x_i}^2 = \sum x_i y_i$

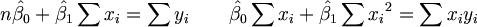
이 식을 풀어서 정리하면,

$\hat{\beta_1} = \frac{S_{(xy)}}{S_{(xx)}} = \frac{ \sum_i \biggl[ (x_i - \overline x)(y_i - \overline y) \biggl] }{ \sum_i{(x_i - \overline x ) }^2 } \qquad \hat{\beta_0} = \overline y - \hat{\beta_1} \overline x$

이를 Python스크립트로 작성하면, SimpleRegressionAnalysis.py